Compound Interest Formula Equals Continuously Compounded Interest
The continuous compound interest formula and its derivation are discussed in this article. The mathematical maximum that compound interest can reach if computed and reinvested into an account's balance for an endless number of periods is known as continuous compounding. In practice, this isn't always doable. In finance, however, the notion of continuously compounded interest is critical. It is, without a doubt, an extreme example of compounding. Because most interest is compounded monthly, quarterly, or semi-annually, this is the case. Continuously compounded interest, in principle, means that a certain account balance earns interest all of the time while also re-adding that interest back into the balance so that it earns interest. Let's have a closer look at the topic and discuss some important questions.
Also read: Difference between Sequence and Series
What is Continuous Compound Interest?
[Click Here for Sample Questions]
Continuous compound interest is the mathematical limit of general compound interest, in which compounding occurs an unlimited number of times every year. Furthermore, with continual compound interest, payments are made at every available time interval.
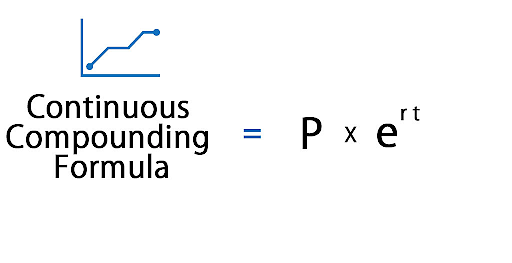
Continuous compounding calculates interest by assuming constant compounding over an infinite number of periods, rather than computing interest over a fixed number of times.
Also read: Frequency Distribution
Continuous Compound Interest Formula
[Click Here for Sample Questions]
A = P × e rt
Where
A = Amount of money after a specific period of time
- P = Principle or the initial amount of money
- e = Napier's number, which is about 2.7183
- r = stands for interest rate and is usually written as a decimal.
- t = denotes the length of time in years.
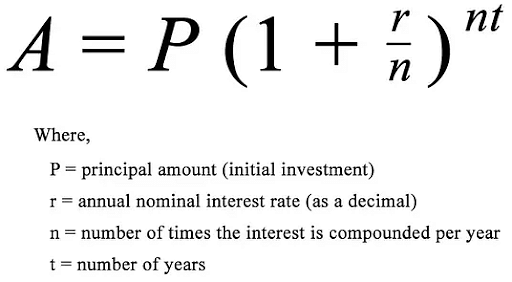
Also read: Measures of Dispersion
Continuous Compound Formula Derivation
[Click Here for Sample Questions]
The continuous compounding formula will be derived from the compound interest formula.
The formula for compound interest is as follows:
A = P (1 + r/n)nt
Here, n denotes the number of terms in which the starting amount (P) is compounding in time t, and A is the ultimate amount (or future value). n is the number for continuous compound interest. As a result, we'll choose n as the limit of the aforementioned calculation.
A= lim P (1 + r/n)nt = Pert
Finally, one of the limit formulae, lim (1 + r/n)n = er, is used.
As a result, the continuous compound interest formula is as follows:
A = Pert
Also read: Relation between Mean, Mode, and Median
Things to Remember
- Compound interest is interest computed on the principal amount of a deposit or loan plus any accrued interest from prior periods.
- Compound interest is computed by multiplying the initial principal amount by one and then multiplying the yearly interest rate by the number of compound periods multiplied by one.
- Compounding interest can occur at any moment, from continually to daily to once a year.
- When computing compound interest, the number of compounding periods makes a significant effect.
- When it comes to compounding profits, time is an added advantage. If you leave your money alone for an extended length of time, it will increase more.
- The key thing is to start and stick with it, regardless of the quantity. Even little monthly payments add up.
Sample Questions
Ques: What Is the Formula for Continuous Compounding? (2 marks)
Ans. When the number of terms is unlimited, the continuous compounding formula is just the compound interest formula. When an amount P is invested for the duration 't' with an interest rate of r percent compounded continuously, the ultimate amount is A = P ert, according to this formula.
Ques: How to Derive Continuous Compounding Formula? (3 marks)
Ans. Remember the compound interest formula: A = P (1 + r/n)nt, where n is the number of terms the original amount (P) is compounding in time t. The ultimate sum is denoted by the letter A. The number of terms in continuous compound interest is limitless, i.e. n. As a result, we'll choose n as the limit of the aforementioned calculation.
A = lim P (1 + r/n)nt = Pert (1 + r/n)n = er)
As a result, the continuous compound interest formula is as follows:
A = Pert
Ques: What is the value of e in the Continuous Compounding Formula? (2 marks)
Ans. The mathematical constant 'e' in the continuous compounding formula has a value of roughly 2.7183. Instead of utilizing the number 2.7183, we may utilize the calculator's 'e' button for more precise calculations.
Ques: An individual invests $1,000 at an annual interest rate of 5% compounded continuously. Find out the final amount you will have in the account after five years? (2 marks)
Ans. The formula for finding the amount in case of continuous compounding is as follows:
A = Pert
A = 1000e(0.05.5)
so, A = 1284.02
Hence, the amount, in this case, is dollars 1284.02.
Ques: Tina put $3000 into a bank that pays an annual interest rate of 7% compounded annually. What is the most amount she may collect from the bank after 5 years? Your answer should be rounded to the closest integer. (3 marks)
Ans: The sum after 5 years is to be found.
P = $3000 is the starting point.
r = 7 percent = 7/100 = 0.07 is the interest rate.
t = 5 years is the length of time.
In the continuous compounding formula, substitute these values.
A = Pert
A = 3000 × e0.07(5) ≈ 4257
The answer is rounded to the closest integer using the calculator.
After 5 years, the total is $4,257.
Ques: Jim put $5000 in a bank that pays a 9% annual interest rate compounded on a daily basis. What is the most amounts he may collect from the bank after 15 years? Your answer should be rounded to the closest integer. (3 marks)
Ans: The sum after 15 years is to be found.
P = $5000 is the starting point.
r = 9 percent = 9/100 = 0.09 is the interest rate.
t = 15 years is the length of time.
In the continuous compounding formula, substitute these values.
A = Pert
A = 5000 × e0.09(15) ≈ 19287
The answer is rounded to the closest integer using the calculator.
After 15 years, the sum is $19,287.
Ques: What should the interest rate be for a $5,300 loan to double in 8 years if the loan is compounded continuously? (4 marks)
Ans: To find: interest rate, r.
P = $5,300 is the starting amount.
A = 2(5300) = $10,600 is the final figure.
t = 8 years is the length of time.
In the continuous compound interest formula,
substitute all of these numbers (8)
A = Pert
10600 = 5300 × er (8)
When both sides are divided by 5300
2 = e8r
Taking both sides of "ln,"
ln 2 = 8r
r = (ln 2) / 8 0.087 by dividing both sides by 8. (using calculator)
As a result, the interest rate is 0.087 x 100 = 8.7.
More Relatable topics to read:
Source: https://collegedunia.com/exams/continuous-compound-interest-formula-with-solved-examples-mathematics-articleid-4740
0 Response to "Compound Interest Formula Equals Continuously Compounded Interest"
Post a Comment